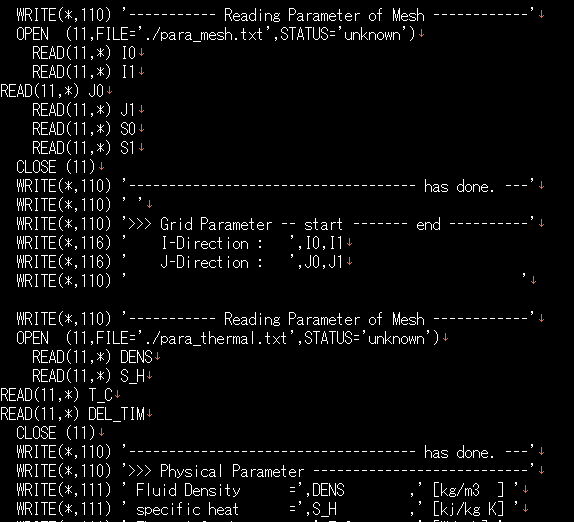
中心差分法や熱伝導方程式について書いてきましたが、今回はエクセルを使って実際に熱伝導方程式を解いていきたいと思います。
計算条件
まず、熱伝導方程式を解くために計算条件を設定します。
定常計算、発熱なし、一次元の熱伝導方程式、境界条件は1000[K]、300[K]で縛ります。
初期温度は0[K]、計算点数は10点で中心差分法を使用します。
0 = k(∂²T/∂x² ) … 一次元の熱伝導方程式
計算手順
この条件をエクセルにプロットしていきます。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 300 |
プロットするとこのような表になると思います。
言葉で詳しく説明すると、境界条件(一番端っこの所)より1 , 10点目は1000 , 300を入力します。
初期条件は0[K]なので2~9点目に0をプロットします。
計算手順2
次に2~9点目に中心差分をした一次元の熱伝導方程式を入れます。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 300 |
| 1000 | 500 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 300 |
中心差分法を導入すると3行目に500, 150が出ます。
この2つの数字は2行目の色のついた値を使い解いてます。
この要領で行を増やしていくと4行目には3点目、8点目、
5行目には4点目、7点目に0以外の数字が表示されます。
そして最終的に全点に数字が表れます。
(100行くらい使えば収束もすると思います)
これで、定常計算、発熱なし、一次元の熱伝導方程式が解けます。
追記
今回は行を使って収束計算しましたが、エクセルのオプション、反復計算設定をすれば数行で収束させれます。
非定常、一次元熱伝導方程式
次に非定常状態の熱伝導方程式も説明したいと思います。
非定常、発熱なし、一次元の熱伝導方程式は以下のようになります。
ρc∂T/∂t = k(∂²T/∂x² ) 非定常一次元の熱伝導方程式
陽解法
非定常つまり時間経過によって値が変化する(時間項が増える)ということです。
上の式でいうと∂T/∂tの部分です。
やはりこの部分も変形しないとプログラムに組み込むことが出来ません。
そこで変形するために使うのが陽解法(陰解法もあるが少し複雑である)です。
変形式は
∂T/∂t = (TN+1 – TN) / Δt
になります。
一次元の熱伝導方程式に代入すると
(TN+1 – TN) / Δt = (k/ρc)*((TN(i+1) – 2TN(i) + TN(i-1)) / Δx²)
となり
TN+1を求めたいので
TN+1 = TN + Δt*((k/ρc)*((TN(i+1) – 2TN(i) + TN(i-1)) / Δx²))
になります。
式だけだと、分かりにくいのでエクセルの場合、どの場所を使えばいいか表で説明します。
| 1 | 2 | 3 | |
| 0秒 | TN(i-1) | 2TN(i) と TN | TN(i+1) |
| 1秒 | TN+1 |
TN+1を求めるのに上の表の場所使って求めます。基本的に求めたいタイムステップの
ひとつ前のタイムステップの値(N+1を求めたいならNの値を使う)を使います。
これを求めたい時間までもっていけば解くことができます。
動画で説明
定常流れになりますが、エクセルで一次元熱伝導方程式を解く方法を紹介します。
因みに筆者が動画を作りました、著作権は問題ないです。
まとめ
エクセルで今回はエクセルを使って実際に熱伝導方程式を解く方法を説明しましたがどうでしたか?
マクロを組まなくても簡単な方程式なら解くことができます。
そして複雑な計算ならやはり、FortranやC言語を使った方が良いです。
関連記事