レイノルズ方程式の一般化
で紹介したレイノルズ方程式をより汎用的に使えるようにすることが、レイノルズ方程式の一般化という事です。
一般化に際しては,次の状況を含めます。
- すきまは2次元的(平面状)である すなわち、奥行き方向にも有限の広がりがある。
- 2面とも移動し、速度をもつ。
- 2面は常に相対的に固定した位置関係を保つのではなく接近速度を持つ。
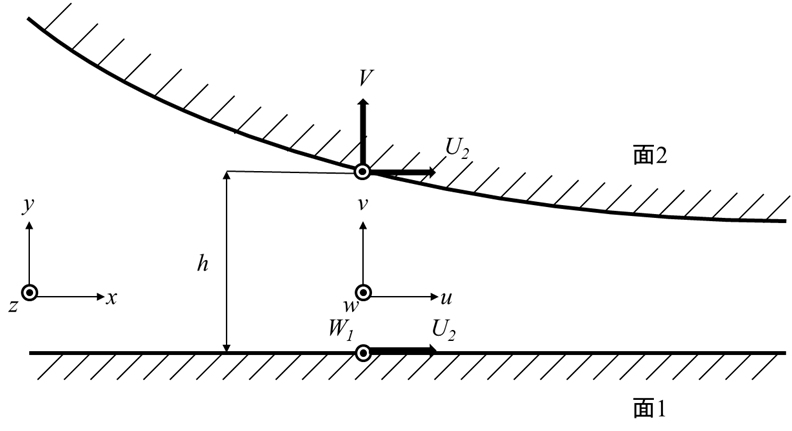
そして下図の座標系を想定すると以下の式が成り立ちます。
∂/∂x(h³/η * ∂p/∂x) + ∂/∂z(h³/η * ∂p/∂z)
=6(U1 – U2) * ∂h/∂x + 6h * ∂(U1 – U2)/∂x + 12h * ∂h/∂t
これが一般的なレイノルズ方程式です。

上式の一般的なレイノルズ方程式の意味について説明します。
左辺には圧力勾配にかかわる項があり、右辺はそれ以外の項で成り立っています。
右辺が油膜内の圧力の発生要因を表し、左辺がその結果として現れる圧力分布の形状を規定している。
右辺の各項については次のような作用があります。
また、右辺の値が負のとき、隙間内には正の圧力が発生します。
くさび膜作用
右辺第1項は下図のように、末狭まり形状(∂/∂x<0)となっているすきまに、壁面の移動に伴って流体が誘いこなれるとき(U1 + U2)、右辺第1項は負になります。

伸縮膜作用
右辺第2項は下図のように壁面の移動速度が流体の進行方向に向かって遅くなっているとき(∂(U1 – U2)/∂x<0)、右辺第2項は負となる。
このような現象は通常発生しないが、圧延加工時の潤滑面を対象としたときなどに起きる場合がある。

絞り膜作用
右辺第3項は下図のように,両面が接近するとき(∂h/∂t<0)、右辺第3項は負となります。
これは,壁面の接近運動がすきま内の潤滑状態を絞り出す際、流体の粘性抵抗に打ち勝つように、すきま内に圧力が発生するからです。

まとめ
この3つの作用を考慮した、レイノルズ方程式を使用することで、より実用的な式になります。
シミュレーションソフトを作成する場合も、こちらの式を使った方がいいと思います。