固体同士の接触
ヘルツの接触(Hertzian contact)理論とは固体同士の接触の中にある理論のことです。
そして、固体同士の接触は、接触表面の形状により面接触(plane contact)、線接触(line contact)および点接触(point contact)の3種類があります。



細かく言うと弾性接触、塑性接触という状態もあるが、大きく大別すると3つに分けられます。
ヘルツの接触(Hertzian contact)理論
ヘルツの接触理論は先程説明した、線接触や点接触の状態になる理論です。
そして、この理論を適用するには次の条件を満たしていないといけません。
接触する固体は等質等方性弾性体であること。
接触する表面は摩擦がなく、また接触域付近では粗さのないなめらかな 2次曲面であること。
接触域は固体の表面に比べて十分に小さいこと。
荷重は接触域に垂直に作用すること。
最初の条件は分かりにくい条件ですがは簡単に言うと、変形する向きによって弾性力が変わらないということです。
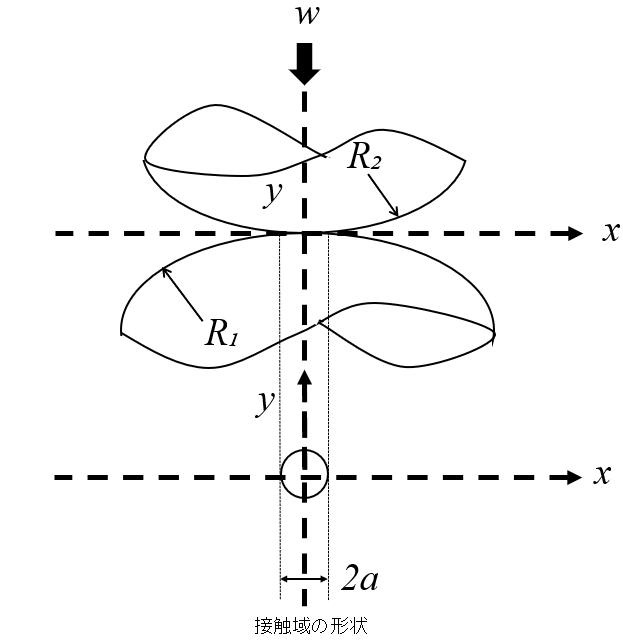
そして、実用上よく利用される形状は「球面同士の接触」や「円筒面同士の接触」がある。なお、「球面同士の接触」は点接触,「円筒面同士の接触」は線接触の代表的形態である。
点接触状態の式
接触域付近において球面形状をもつ2つの弾性体(曲率半径:R₁、R₂・ヤング率・ポアソン比V₁、V₂)に,接触域に対して垂直に作用する荷重Wが負荷されると、接触域の形状は円形になります。このときの接触圧力分布は半だ円体状となり、接触面内の位置A(x、y) における接触圧力pは次式で表されます。
p=pMax√1 – (x/a)² – (y/a)²
ここでのaは接触半径、pMaxは接触圧力の最大値で次式で表せます。
a = (3WR/2E’)1/3
pMax = 2W/2πa² = 3/2 * pmean

上の式で不明な文字E’は等価ヤング率(reduced Young’smodulus)、Rは等価曲率半径(reduced radius of curvature)、pmeanは平均接触圧力(average contact pressure)と呼ばれ、それぞれ次式で表されます。
1/E = 1/2 *((1-v²)/E₁ + (1-v²)/E₂)
R = R₁*R₂ / (R₁ + R₂)
pmean = W/(πa²)
最後にこれらの数値を組み合わせると、変形量δが表せます。
δ = (9W² / 4E’R)1/3
これがヘルツの接触理論になります。
ヘルツの接触理論をプログラムしてみた
実際にフォートランを使ってヘルツの接触圧をプログラミングしてみました。
式はp=W/(πa²) * √1 – (x/a)²
a = (3WR/2E’)1/3
を使います。
具体的な数字は
| E’:ヤング率 | 1.31×10² [GPa] |
| R:円の半径 | 10 [mm] |
| W:線荷重 | 50 [kN] |
です。
計算結果は下図になります。

中央が1番圧力が出てますね。
中央が1番変形しているので、当たり前な事とも言えますが(笑)
プログラムコードも載せようか迷ってますが、文字が多くなるので需要があるのであれば載せようと思います。
まあ、ないと思いますが(笑)
まとめ
筆者がヘルツの接触理論を扱っていて思った事はそんなに難しい理論ではないかなと思います。
むしろこの理論を基本に研究が積みあがっているように感じます。
弾性流体潤滑(EHL)なんかはまさにそれに該当します。
関連記事